Тверь какой район: список с границами на карте города, подробное описание, где лучше жить

Содержание

Тверской район Центрального административного округа (ЦАО) города Москвы

  • Характеристика
  • Органы власти
  • Улицы района
  • Документы
  • История
  • Официальные символы

Характеристика

Тверской район входит в состав 10-и районов Центрального административного округа города Москвы.
Район занимает территорию в 565 гектаров в нём
насчитывается 179 улиц и 16 станций метро (Белорусская, Белорусская, Достоевская, Китай-город, Китай-город, Лубянка, Маяковская, Менделеевская, Новослободская, Охотный ряд, Площадь Революции, Пушкинская, Тверская, Театральная, Цветной бульвар и Чеховская). Численность проживающего здесь населения составляет порядка 76 тысяч человек.
Управление районом осуществляет Управа Тверского района и прочие районные органы власти.

 

Карта Тверского района города Москвы

Для корректной работы онлайн карты необходима поддержка javascript!

Описание района

Район получил своё название от главной Московской магистрали — Тверской улицы. Сегодня это один из самых перспективных сегментов столичного мегаполиса. История московского центра и его традиции неотделимы от истории этого района.

Уровень развития инфраструктуры Тверского района соответствует статусу главного района Москвы. Здесь особенно сильно наблюдается явление, так называемой «суточной миграции», когда дневное «население» района в 7—8 раз превышает постоянное. Поблизости от Тверской улицы с трудом можно найти тихие переулки — сказывается высокая концентрация офисов. Повсюду люди, спешащие на работу или учёбу, а также туристы приехавшие осмотреть местные достопримечательности. Поэтому инфраструктура района, призвана удовлетворять потребности и желания не только жителей, но и гостей района. Цены на продукты питания здесь значительно выше, чем в других районах Москвы.

Большие трудности Тверской район испытывает с парковочными местами, в часы пик нередки заторы и пробки.

Связанные документы

Распоряжение Правительства Москвы № 497-РП от 28 июня 2011 года
О мерах по дальнейшей реализации инвестиционного проекта строительства пристройки к медицинскому центру по адресу: ул. 3-я Тверская-Ямская, вл.30/29
Распоряжение Правительства Москвы № 422-РП от 31 мая 2011 года
Об оказании содействия в подготовке и проведении на Красной площади 12 июня 2011 г. праздничного концерта
Постановление Правительства Москвы № 140-ПП от 14 апреля 2011 года
О мерах по дальнейшей реализации инвестиционного проекта по адресу: ул.Б.Дмитровка, д.18/10, стр.2
Распоряжение Правительства Москвы № 164-РП от 9 марта 2011 года
О передаче в федеральную собственность нежилых помещений по адресу: Старая площадь, д.10/4, стр.1 и нежилого здания по адресу: Старая площадь, д.6, стр.1
Распоряжение Правительства Москвы № 120-РП от 15 февраля 2011 года
О мерах по завершению реализации инвестиционного проекта по адресу: ул.Тверская, вл.16/2, стр.2

Все документы (165)

Граница района

Граница Тверского района проходит: по оси Моховой улицы, далее по осям: Большой Никитской улицы и Газетного переулка, по юго-западным границам владений №№ 15 и 13/15 по Газетному переулку и владений №№ 8/10 (к.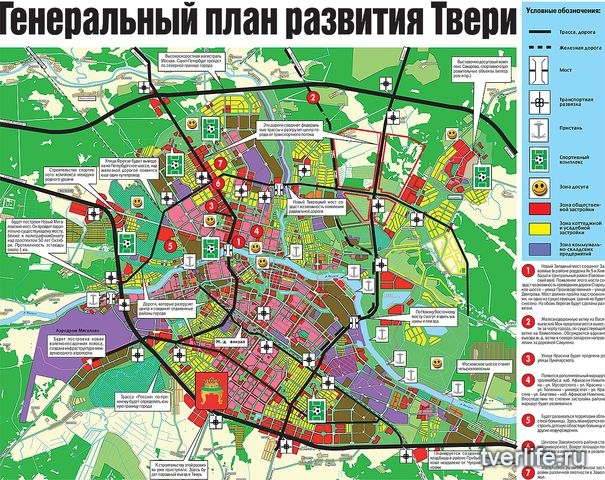 2 и 1) по Брюсову переулку, далее, пересекая Брюсов переулок, по северо-восточным границам владения № 17 по Брюсову переулку и владений №№ 20 (к. 3 и 2) по Вознесенскому переулку, оси Вознесенского переулка, северо-восточным границам владения № 17 по Вознесенскому переулку и владения № 18 по Леонтьевскому переулку, осям: Леонтьевского и Большого Гнездниковского переулков, северо-восточной границе владения № 24 по Тверскому бульвару, оси юго-западного проезда Тверского бульвара, далее, пересекая Тверской бульвар, по осям: Сытинского, Большого Палашёвского, Трёхпрудного и Благовещенского переулков, юго-западным границам владения № 1 по Благовещенскому переулку, северо-восточным границам территории сада «Аквариум», далее, пересекая Большую Садовую улицу, по осям: 2-й Брестской улицы и улицы Грузинский вал, далее по северо-восточным границам владений №№ 9—11 по улице Грузинский вал, далее, пересекая Смоленское направление и Алексеевскую железнодорожную ветку Московской железной дороги (МЖД), северо-западной границе полосы отвода Алексеевской соединительной железнодорожной ветки МЖД, осям: улицы Сущёвский вал, Тихвинской улицы и Перуновского переулка, юго-западной границе площади Борьбы, оси улицы Достоевского, юго-западной границе Суворовской площади, осям: Самотёчной и Садовой-Самотечной улиц, западного проезда Цветного бульвара, далее, пересекая Трубную площадь, по осям: западного проезда Неглинной улицы, Неглинной улицы, Театрального проезда, северо-западным и северо-восточным границам Лубянской площади, оси Лубянского проезда, юго-восточным границам Славянской площади и площади Варварские Ворота, оси Китайгородского проезда, оси русла реки Москвы, оси Большого Каменного моста, юго-западной границе Боровицкой площади до Моховой улицы.

Соседние районы

Районы Москвы имеющие общую границу с Тверским районом:
Арбат,
Басманный,
Беговой (САО),
Бутырский (СВАО),
Замоскворечье,
Красносельский,
Марьина роща (СВАО),
Мещанский,
Пресненский,
Савёловский (САО),
Таганский,
Хамовники и
Якиманка.

 

Районы Центрального округа Москвы

Список районов ЦАО:
Арбат,
Басманный,
Замоскворечье,
Красносельский,
Мещанский,
Пресненский,
Таганский,
Тверской,
Хамовники и
Якиманка.

 

Административные округа Москвы

  • ЦАО
  • САО
  • СВАО
  • ВАО
  • ЮВАО
  • ЮАО
  • ЮЗАО
  • ЗАО
  • СЗАО
  • ЗелАО

Информация о районе

Адрес: 170042, г.Тверь, ул. Горького, д.130

тел/факс 8 (4822) 52-15-61

Адрес электронной почты:

[email protected]

Справка о Заволжском районе.

Образованный в 1936 году, Заволжский район занимает территорию около 70 квадратных километров. Здесь проживает около 148 тысяч человек, из которых 31 тысяча — дети до 18 лет, 41 тысяча — пенсионеры. Современное Заволжье — это и памятники старины, и большие промышленные предприятия, это новые микрорайоны и тихие улочки, застроенные одноэтажными деревянными домами. Это люди, которые здесь живут, работают и считают этот район лучшим в нашем городе.

История Твери и тверского Заволжья неразрывно связаны. Более 500 лет назад от этих волжских берегов отправился в свое путешествие за три моря наш земляк — купец Афанасий Никитин. Сегодня памятник первому европейцу, посетившему Индию и открывшему ее для соотечественников, — одна из главных достопримечательностей города, эмблема Заволжского района.

Тверское Заволжье можно с полным правом назвать одним из наиболее промышленно развитых районов города. Предприятия, расположенные в этом районе, производят более 40% от общего объема продукции, выпускаемой в Твери.

Самым крупным предприятием не только Заволжья, но и всего нашего города является Тверской вагоностроительный завод, основанный еще в 1898 году франко-бельгийским акционерным обществом «Диль и Бакалан». В настоящее время завод специализируется на выпуске пассажирских вагонов, которые сегодня можно увидеть на всех железных дорогах страны. Промышленность Заволжья также представлена такими крупными предприятиями, как «Центросвармаш», «Тверьстеклопластик», «КСМ-2», «Тверской завод ячеистого бетона», «Тверской стекольный завод», «Юнайтед боттлинг груп» («UBG»), Тверской лакокрасочный завод, ТЭЦ-3.

В районе насчитывается более 500 предприятий малого бизнеса и более 1800объектов потребительского рынка.

В сфере науки и техники успешно работают «ЦКБ транспортного машиностроения», Тверской институт вагоностроения, Институт механизации льноводства.

На территории Заволжского района располагаются три федеральных высших учебных заведения — Тверской государственный технический университет, Тверская сельскохозяйственная академия, а так же корпуса Тверского государственного университета, который в ближайшие годы «переедет» на Соминку. Здесь будет построен студенческий городок со всей необходимой инфраструктурой. В районе находятся также четыре учреждения среднего профессионального образования, 17 общеобразовательных школ и 33 дошкольных учреждения.

Год от года растет количество предприятий торговли, бытового обслуживания, общественного питания, расширяется сеть спортивных и культурных учреждений. Большой популярностью у спортсменов и любителей активного отдыха пользуются недавно построенные спорткомплексы «Юность» и «Орбита» с ледовыми площадками.

На территории района находится более 400 объектов улично-дорожной сети (улиц, площадей и т.д.), расположены более 8000 жилых домов, в том числе 849 многоквартирных.

К числу наиболее важных задач, которые необходимо решать областным и муниципальным властям, можно отнести:

· ремонт существующих и строительство новых современных автодорог, мостов, соединяющих между собой отдельные микрорайоны;

· ремонт, проектирование и строительство инженерных сетей электро- и теплоснабжения, канализации, систем водоотведения в микрорайонах индивидуальной застройки;

· продолжение реализации программы капитального ремонта многоквартирных жилых домов;

· ремонт внутриквартальных дорог и благоустройство придомовых территорий;

· развитие сети учреждений дошкольного и среднего образования.

 

Что такое Площадь?

Площадь равна площади поверхности!

Пример:

Все эти фигуры имеют одинаковую площадь 9:

 

Это помогает представить , сколько краски покроет фигуру.

Площадь простых фигур

Для некоторых фигур существуют специальные формулы:

Пример: Какова площадь этого прямоугольника?

Формула:

Площадь = w × h
w = ширина
h = высота

Ширина равна 5, а высота равна 3, поэтому мы знаем, что w = 5 и h = 3 :

Площадь = 5 × 3 = 15

Узнать больше в области плоских форм.

Площадь путем подсчета квадратов

Мы также можем поместить фигуру в сетку и подсчитать количество квадратов:

Площадь прямоугольника 15

сторона, то площадь равна 15 м 2 (15 квадратных метров)

Квадратный метр по сравнению с квадратным метром

Базовой единицей площади в метрической системе является квадратных метров , это квадрат со стороной 1 метр:

1 квадратный метр

Будьте осторожны, чтобы сказать «квадратные метры», а не «метры в квадрате»:

Существуют также «квадратные мм», «квадратные сантиметры» и т. д., узнайте больше на Метрическая площадь.

Приблизительная площадь при подсчете квадратов

Иногда квадраты не совсем соответствуют форме, но мы можем получить «приблизительный» ответ.

В одну сторону:
  • больше чем половина квадрата считается за 1
  • меньше половина квадрата считается за 0

Вот так:

Площадь этого пятиугольника равна приблизительно 17

 
Или мы можем считать один квадрат, когда кажется, что

площадей составляют .

Пример: Здесь площадь, отмеченная « 4 «, кажется равной примерно 1 целому квадрату (также для « 8 «):

Площадь этого круга равна приблизительно 14 формула (когда это возможно) лучше всего:

Пример: Круг имеет радиус 2,1 метра:

Формула:

Площадь = π × r 2

Где:

    9008 пи (3,1416. ..)
  • r = радиус

Радиус равен 2,1 м , поэтому:

Площадь = 3,1416… × (2,1 м) 2

= 3,1416… × (2,1 м × 2,1 м)

103,088 = m 2

Таким образом, площадь круга равна 13,85 квадратных метров (с точностью до 2 знаков после запятой)

Площадь сложных фигур

Иногда мы можем разбить фигуру на две или более более простые фигуры:

Пример: Какова площадь этой формы?

Разобьем площадь на две части:

Часть А представляет собой квадрат:

Площадь A = a 2 = 20 м × 20 м = 400 м 2 Часть B представляет собой треугольник. Если смотреть сбоку, то его основание 20 м, а высота 14 м.

Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м 2

Площадь = 540 м 2

Площадь путем сложения треугольников

Мы также можем разбить фигуру на треугольники:

 

Затем измерьте основание ( b ) и высоту ( h ) каждого треугольника:

 

Затем вычислите каждую площадь
(используя Площадь = ½b × h) и сложите их все.

 

Площадь по координатам

Когда мы знаем координаты каждой угловой точки, мы можем использовать метод площади неправильных многоугольников.

Область многоугольника с помощью инструмента рисования также может помочь.

 

 

Деятельность в области сада

Что такое площадь в математике? Определение, формулы, формы, примеры

Определение

Определение

Площадь определяется как общее пространство, занимаемое плоской (двухмерной) поверхностью или формой объекта.

Возьмите карандаш и нарисуйте квадрат на листе бумаги. Это двумерная фигура. Пространство, которое фигура занимает на бумаге, называется ее 9.0245 Зона .

Теперь представьте, что ваш квадрат состоит из меньших квадратов. Площадь фигуры рассчитывается как количество единичных квадратов, необходимых для покрытия общей площади поверхности этой конкретной двумерной формы. Квадратные сантиметры, квадратные футы, квадратные дюймы, квадратные метры и т. д. являются одними из распространенных единиц измерения площади. Чтобы узнать площадь квадратных фигур, нарисованных ниже, нарисуйте единичные квадраты со стороной в 1 сантиметр. Таким образом, форма будет измеряться в см² , также известных как квадратные сантиметры.

Здесь площадь фигур ниже будет измеряться в квадратных метрах (м²) и квадратных дюймах (дюйм²).

Как вычислить площадь, если в сетке есть еще и полединичные квадраты?

Чтобы понять это, давайте возьмем еще один пример:

Шаг 1 : Подсчитайте полные квадраты.

Есть 18 полных квадратов.

Шаг 2: Сосчитайте половинки квадратов.

Подсчитав, мы видим, что полуквадратов 6.

Шаг 3: 1 полный квадрат $= 1$ квадратная единица

Итак, 18 полных квадратов $= 18$ квадратных единиц

1 половина квадрата $= \frac{1}{2}$ квадратная единица

6 половинных квадратов $= 3$ квадратных единиц

Общая площадь $= 18 + 3 = 21$ квадратных единиц.

Происхождение термина: Район

Термин «район» происходит от латинского языка, что означает «простой кусок пустой земли». Это также означает «определенное количество пространства, содержащееся в наборе границ».

Подробнее о Зоне

Посмотрите на ковер в вашем доме. Чтобы купить ковер, подходящий к полу, нам нужно знать его площадь. Или ковер будет больше или меньше, чем пространство! Некоторые другие случаи, когда нам нужно знать площадь, — это при укладке плитки на пол, покраске стены или наклеивании на нее обоев или определении общего количества плиток, необходимых для строительства бассейна.

Формулы для вычисления площади

Нас окружает множество двумерных фигур: круг, треугольник, квадрат, прямоугольник, параллелограмм и трапеция. Вы можете нарисовать все эти фигуры на бумаге. Каждая фигура уникальна и уникальна, поэтому ее площадь также рассчитывается по-разному. Чтобы найти площадь, сначала определите форму.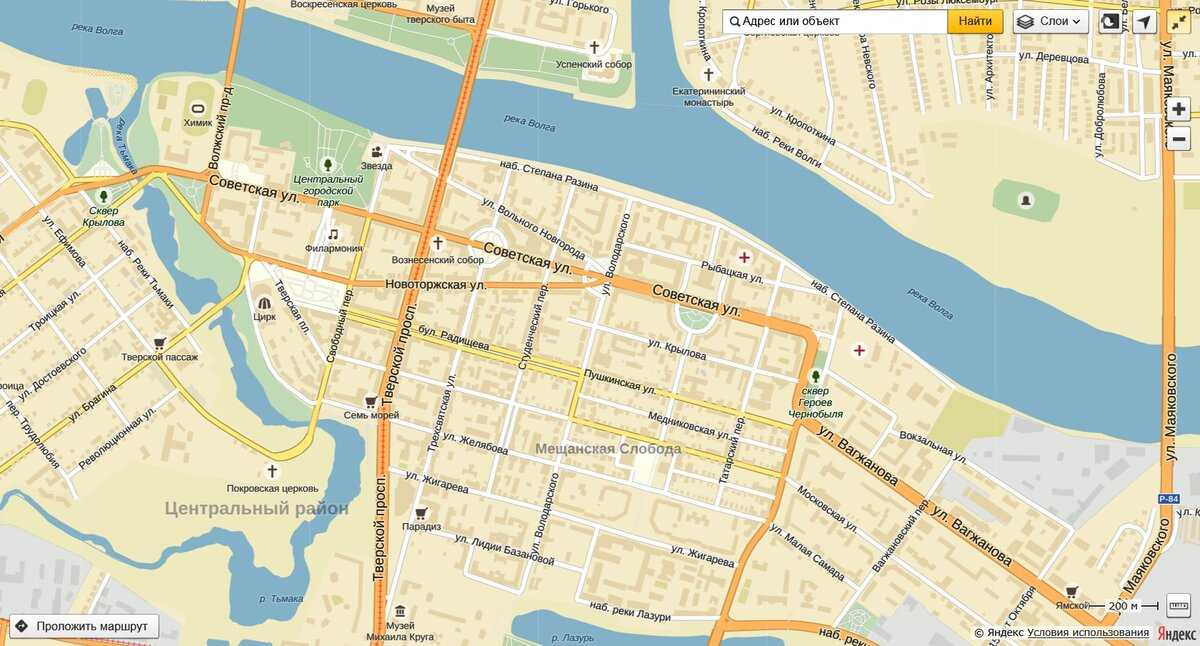 Затем используйте соответствующую формулу из списка, приведенного ниже, чтобы найти его площадь.

Области составных фигур

Каждая плоская фигура не может быть классифицирована как простой прямоугольник, квадрат, треугольник или типичная форма в реальной жизни. Некоторые фигуры состоят из нескольких простых двумерных фигур. Соединим прямоугольник и полукруг.

Эти фигуры, образованные комбинацией двух или более простых фигур, называются « составные фигуры » или «составные фигуры ».

Чтобы найти площадь составной фигуры, мы должны найти сумму площадей всех фигур в ней. Таким образом, площадь фигуры, которую мы только что нарисовали, будет равна площади прямоугольника, l$\times$ b плюс половина площадь круга, ½ x πr² , где l и b — длина и ширина прямоугольника, r — радиус прямоугольника полукруг.

Если мы нарисуем полукруг под треугольником, мы получим составную фигуру:

Площадь такой составной фигуры будет вычислена путем сложения площади треугольника и площади полукруга. 2$)

, где r — радиус полукруга, а b и h — основание и высота треугольника соответственно.

Применение в реальной жизни

Вот несколько способов применения знаний о площади фигур в повседневной жизни.

  • Мы можем найти площадь подарочной бумаги, чтобы проверить, сможет ли она покрыть коробку или нет.
  • Мы можем найти площадь квадрата или круга, чтобы найти площадь сигнального щита.

    • 9{2}$

    Заключение

    С помощью SplashLearn обучение становится частью жизни детей, и их поощряют учиться каждый день. Платформа делает это с помощью интерактивных игр и забавных рабочих листов. Для получения дополнительной информации об увлекательных математических играх посетите сайт www.splashlearn.com.

    Связанный математический словарь Узнайте больше о таких понятиях, как ‘ Периметр , Многоугольник , Square Unit , Unit Square ’ и другие интересные математические темы на сайте www. SplashLearn.com.

    Часто задаваемые вопросы

    Чем отличаются периметр и площадь фигуры?

    Периметр и площадь связаны с двумерной геометрией форм. Периметр — это общая длина контура вокруг фигуры, а площадь — это общее пространство внутри фигуры.

    Почему площадь измеряется в квадратных единицах, а периметр — нет?

    Площадь — это мера количества единичных квадратов, вписывающихся в двумерную форму, поэтому она выражается в квадратных единицах. Периметр является мерой длины контура фигуры и выражается в линейных единицах.

    Каково значение концепции области обучения?

    Знание площади формы дает учащимся четкое представление об общем пространстве, охватываемом границами этой формы. Эта концепция имеет множество практических применений, таких как определение площади ковра в комнате, определение общего размера стены, которую нужно покрасить, и т.